換算質量

「ランダウ＝リフシッツ物理学小教程 力学・場の理論」51頁の§11."換算質量"をフォローします
相互作用する二つの質点からなる系の運動（二体問題）を，慣性中心を原点として中心対称な外場Uの中で運動する質量mの一質点の運動と見做すことができます
このmを換算質量（reduced mass）と呼びます

reduced mass.wxm

r1, r2 : 二つの質点の位置ベクトル(%o2, %o3)
v1, v2 : 二つの質点の速度ベクトル(%o4, %o5)
%i1にて位置ベクトルの成分が時間 t に依存することを宣言します（画面出力は省略）
二つの質点相互の相対位置ベクトルrを%o6式に示します
rの微分を相対速度ベクトルvとして%o7式に示します

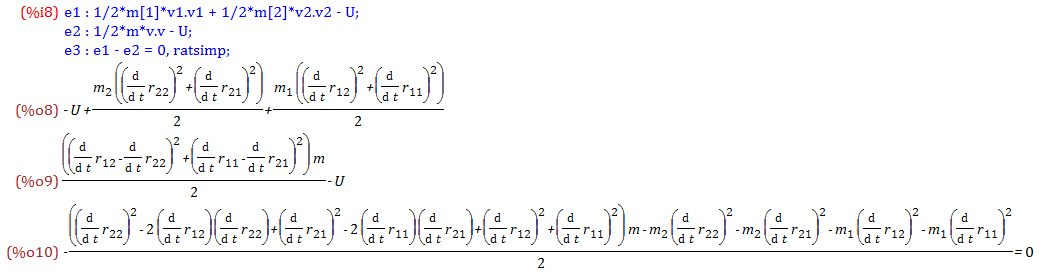
系のラグランジアンを%o8式に示します
換算質量mの一質点のラグランジアンを%o9式に示します
上2式が一致するとした場合%o10式が成り立ちます

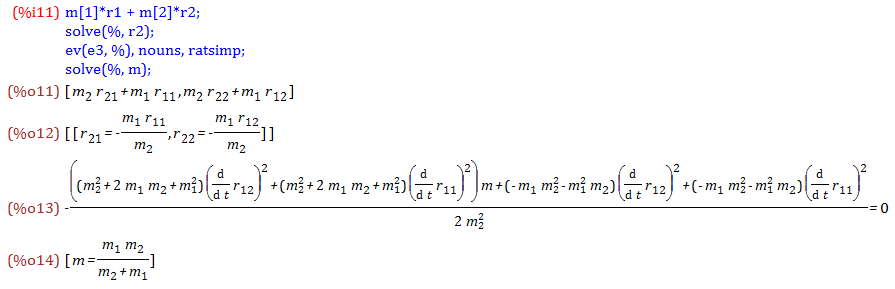
座標原点を慣性中心にとると%o11式が成り立ちます（ = 0(零ベクトル)は省略）
上式をr2について解いた結果を%o12式に示します
これを%o10式に代入してまとめると%o13式を得ます
これをmについて解いた結果を%o14式に示します

ということで，換算質量は2つの質量の調和平均（harmonic mean）の1/2に相当します

力学・場の理論―ランダウ=リフシッツ物理学小教程 (ちくま学芸文庫)