前回に引き続き,ガロア理論を用いて「4次方程式の可解性」がどのように確認出来るのかを見てみます
galois_theory2.wxm

一般の4次方程式について考えますので,次数 N に4を代入します(%o1)
最高次の係数を 1 とした4次方程式を%o3に示します
この方程式の解を α1~4 とし,1次式の積と同一視します(%o4)
これより方程式は4つの解の入れ替えに対して不変であることが解ります
【対称群S4】

4次対称群 S4 は4つの要素の置換全体からなる群で,その位数は 4! = 24 です
これらの元を置換行列で出力した s1~s24 を配列としてまとめて S4 に代入します(%o7)

いま In に配列 {1,2,3,4} を代入します(%o9)
In に左から s1~s24 をそれぞれ作用させてちゃんと入れ替えがなされるかを確認します(%o10)
この結果を見ながら s1~s24 を分類していきます

関数をまとめてこのブロックで定義しておきます(画面出力は省略)
cl(L) : 配列 L を引いて複製した配列を返します
ml(c, n) : c_i を要素として i = 1~n の配列を返します
trans(L, i, j) : 配列 L に対して i 番目と j 番目の互換を返します
cycle3(L, i, j, k) : 配列 L に対して i→j→k→i の巡回置換を返します
cycle4(L, i, j, k, l) : 配列 L に対して i→j→k→l→i の巡回置換を返します
i_list(L, a) : 配列 L に対して要素 a が含まれるインデックスを返します
【恒等置換】

まず s1 は入れ替え無しなので e となります(%o18)
ここで e は恒等置換です
【互換】
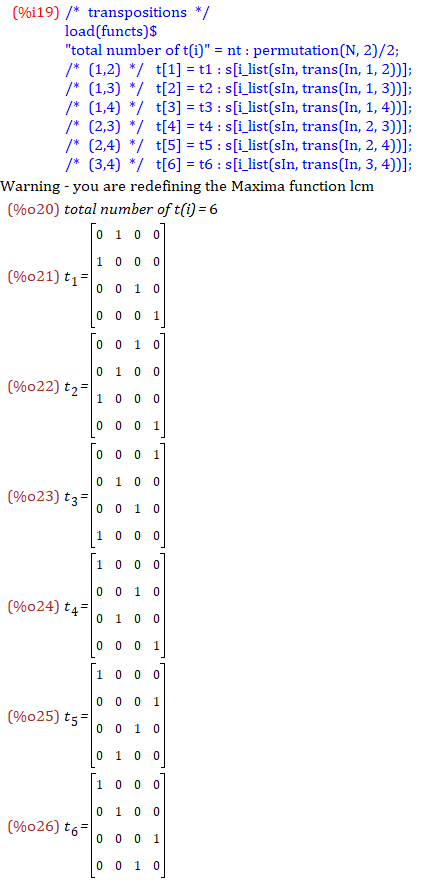
互換は (1,2),(1,3),(1,4),(2,3),(2,4),(3,4) の6つです
t1~t6 に対応するS4の元をそれぞれ代入します(%o21~26)
【巡回置換】

3つの巡回置換は (1,2,3),(1,3,2),(1,2,4),(1,4,2),(1,3,4),(1,4,3),(2,3,4),(2,4,3) の8つです
p1~p8 に対応するS4の元をそれぞれ代入します(%o28~35)

4つの巡回置換は (1,2,3,4),(1,2,4,3),(1,3,2,4),(1,3,4,2),(1,4,2,3),(1,4,3,2) の6つです
q1~q6 に対応するS4の元をそれぞれ代入します(%o37~42)
【互いに素な互換の積】

互いに素な互換の積は (1,2)(3,4), (1,3)(2,4), (1,4)(2,3) の3つです
u1~u3 に対応するS4の元をそれぞれ代入します(%o44~46)
【交代群A4】

S4 の部分群 A4 は交代群(偶置換のみからなる部分群)で,位数は 12 です
A4 の元は {e, p1~p6, u1~u3} です(%o47)
p1~p6 及び u1~u3 が偶置換であることをそれぞれ確認します(%o49~59)
【クラインの4元群V】

A4には部分群としてクラインの4元群Vが存在します(位数は当然 4 です)
V の元は {e, u1~u3} です(%o60)
u1~u3 が偶置換であることは%o57~59で確認済みです
【自明な部分群E】

E の元は {e} です(%o62)
E も V の正規部分群です(E ◁ V)

交代群 A4 は S4 のすべての元 g に対して g.A4.g^-1 = A4 が成り立ちます(%o66)
したがって A4 は S4 の正規部分群です(A4 ◁ S4)

4元群V は A4 のすべての元 g に対して g.V.g^-1 = V が成り立ちます(%o69)
したがって V は A4 の正規部分群です(V ◁ A4)
可解性の確認
S4 は次のような正規列を持っています: E ◁ V ◁ A4 ◁ S4
V は位数 4 の巡回群であり,これは可解群です

%o73より剰余群 S4/A4 は位数 2 の巡回群であり,これも可解群です

%o77より剰余群 A4/V は位数 3 の巡回群であり,これも可解群です
よって E ◁ V ◁ A4 ◁ S4 はアーベル正規列を形成し,各剰余群も可解であるためS4自体が可解群となります
ということで,一般の4次方程式の可解性が確認されました
