今回は4節点アイソパラメトリック要素のFEMを使って以下の例題を解いてみます
E，νは要素内で一定かつ等方性とします
iso-parametric 4-node sample1.wxm
n : 節点数
NN : 形状関数
J : Nxのヤコビ行列
J_i : Jの逆行列（invert）
j : Nxのヤコビアン（det(J））
形状関数やヤコビアン等を一通り代入します（画面出力は省略）
B : Bマトリックス
D : Dマトリックス
Ke : 要素剛性マトリックス
Keの導出については4節点アイソパラメトリック要素 その4を参照ください（画面出力は省略）
幾何学的境界条件を与えます
全体節点変位ベクトルUを%o22式に，未知節点変位ベクトルUaを%o24式にそれぞれ示します
力学的境界条件を与えます
全体節点荷重ベクトルFを%o29式に示します
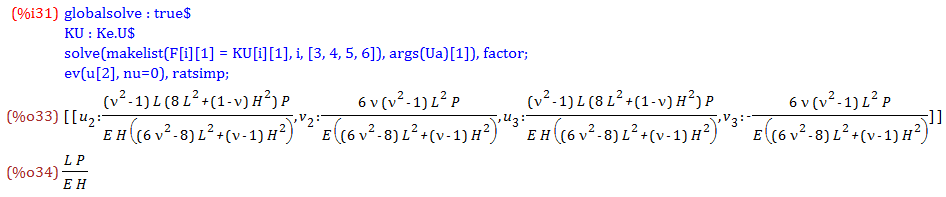
F = K.U の連立方程式を，Uaについて解いた結果を%o33式に示します
（globalsolve:trueの宣言により，解は変数に代入されます）
ここでν= 0とした場合のu2（=u3）は%o34式となり，公称歪P/(E*H)をLで積分した値と一致します
%o33式の結果を使って未知のF（反力）を計算します（%o35〜38）
%o39式より，x方向の反力が外力(+P)と釣合っていることが解ります
また%o40式より，y方向の反力が釣合っていることが解ります
具体的に応力ベクトルを計算し，相当応力をプロットしてみます
寸法や材料定数など適当な値を代入します
応力ベクトルtを%o49式に示します
平面応力状態におけるMises相当応力が自然座標rの関数となっていることが解ります（%o50）
求めたMises相当応力を横軸にr1，縦軸にr2として%t51にプロットします
