相対性理論 その5 （E=mc2）

相対論的力学（relativistic dynamics）についてのお話です
「ランダウ＝リフシッツ物理学小教程 力学・場の理論」208頁の§39."エネルギーと運動量"をフォローします
自由粒子の作用積分について考えます
（テキストは任意の速度ベクトルを与えていますが，ここでは一軸上の運動とします）
special relativity4.wxm

c : 真空中の光速度
v : 自由粒子の速度
L : 自由粒子の相対論的ラグランジアン
t1, t2 : それぞれ粒子の運動の始点と終点の時刻
自由粒子に対する作用はローレンツ変換に対して不変となることが要請されるため，世界間隔dsに謎の定数-m*cを掛けた積分の形を取り，時間についての積分に書き直した%o6式で表されます
また作用の一般的な定義を%o7式に示します

%o6, 7式からLは%o8式と表されます
これをv/cについてテイラー展開し，高次の項を捨てると%o9式を得ます
ラグランジアンの中の定数項は運動方程式に影響しないのでこれを除くと%o10式となり，古典論に帰着します
（これより定数mは自由粒子の質量と一致します）

粒子の運動量pの定義を%o11式に示します
これに%o8式を代入して偏微分を計算すると%o12式を得ます
（v/c << 1であれば p = m v となり古典論的運動量と一致します）

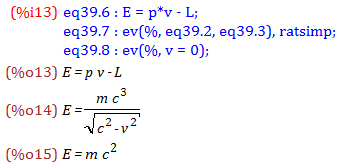
粒子の全エネルギーの一般的な定義を%o13式に示します（余談ですが，上式はハミルトニアン（Hamiltonian）と呼ばれます）
これに%o8式および%o12式を代入してまとめると%o14式を得ます
相対論的力学では v = 0 としても粒子エネルギーはゼロとはならず，%o15式の値に留まります

これを粒子の静止エネルギー（rest energy）と呼びます
アインシュタインといえばコレ，と言われるくらい有名な式ですねヽ( ´ー`)ノ

力学・場の理論―ランダウ=リフシッツ物理学小教程 (ちくま学芸文庫)