前回FFTに使ったサンプルデータについての説明です
まずはサンプリング元となる波形を,複数の正弦波を重ね合わせて作成します
fft2.wxm

n : 正弦波の数
f : 振動数の配列[Hz]
a : 振幅の配列
φ : 位相の配列[rad]
C : 定数項(振幅)
%o1のfpprintprec : 3 は表示桁数の宣言です(画面出力は省略)
重ね合わせる正弦波の数は3とします(%o2)
f, a, φ, C をそれぞれ%o3〜6式に示します
3波を合成した式をLoとして%o7式に示します

Loを横軸にt, 縦軸に振幅として0〜0.6[s]の間で%t8にプロットします
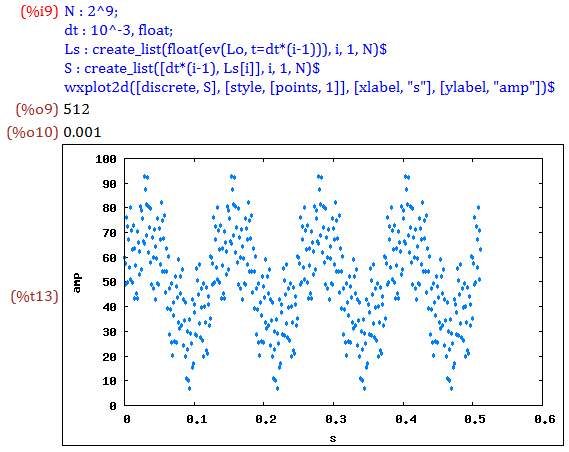
Loの波形のサンプリングを行います
サンプル数Nとサンプリング間隔dtをそれぞれ%o9, 10式に示します
サンプリングした振幅を配列としてLsに代入します(%o11)(画面出力は省略)
Lsとサンプリング時刻tで二次元配列Sを作成します(%o12)
これを横軸にt, 縦軸に振幅として%t13にプロットします
ということで,前回のFFTの結果と%o3式が合っていることが解ります