変位型の有限要素法では要素を構成する節点の変位で構造物の変形を表しますが，要素内の任意の点における変位は節点変位からの内挿（interpolation）により与えられます
この内挿に用いる関数を形状関数（shape function）と呼びます
ここでは1次元要素の形状関数を求めます
shape function1.wxm
【2節点要素】（L）
n : 節点数
N : 形状関数
nに節点数2を代入します（%o1）
変位uを自然座標r1の1次関数で仮定します（%o2）
各節点の自然座標を-1, 1で与え，未定係数配列で括ったマトリックスのinverseを%o5式に示します
変位uを未定係数配列で括ったベクトルと上式との線形変換をまとめると形状関数を得ます（%o6）
Nの総和は1となります（%o7）
横軸をr1として形状係数を%t8, 9にそれぞれプロットします
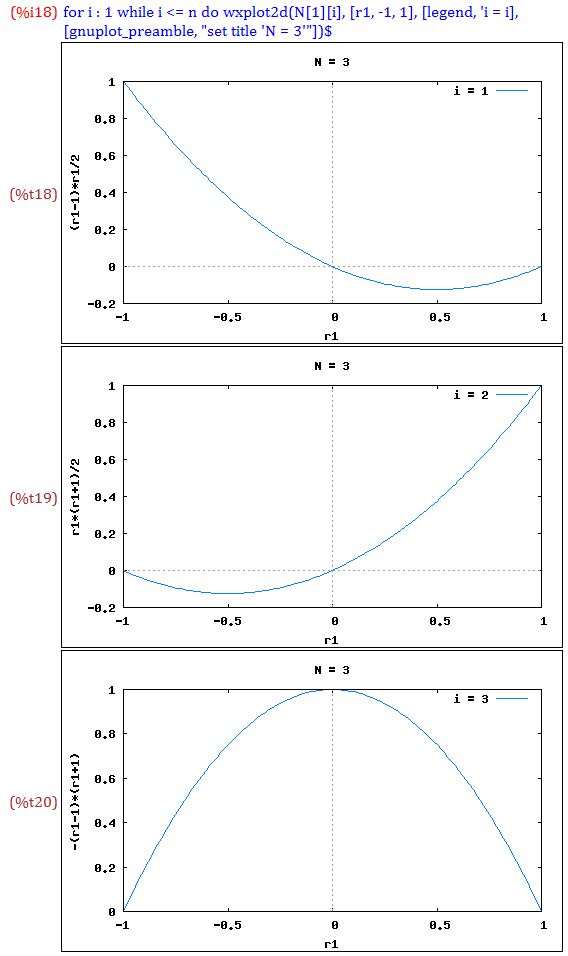
【3節点要素】（L）
同様にしてnに節点数3を代入します（%o10）
変位uを自然座標r1の2次関数で仮定します（%o11）
各節点の自然座標を-1, 1, 0で与え，未定係数配列で括ったマトリックスのinverseを%o15式に示します
変位uを未定係数配列で括ったベクトルと上式との線形変換をまとめると形状関数を得ます（%o16）
Nの総和は1となります（%o17）
同様にして形状係数を%t18〜20にそれぞれプロットします
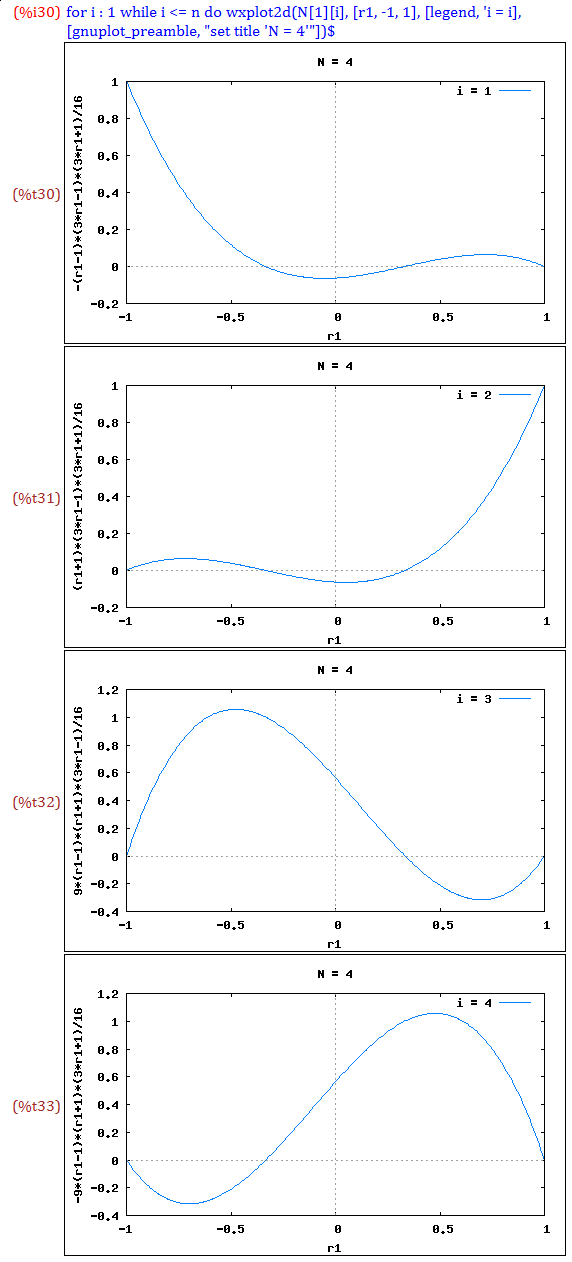
【4節点要素】（L）
同様にしてnに節点数4を代入します（%o21）
変位uを自然座標r1の3次関数で仮定します（%o22）
各節点の自然座標を-1, 1, -1/3, 1/3で与え，未定係数配列で括ったマトリックスのinverseを%o27式に示します
変位uを未定係数配列で括ったベクトルと上式との線形変換をまとめると形状関数を得ます（%o28）
Nの総和は1となります（%o29）
同様にして形状係数を%t30〜33にそれぞれプロットします
各要素名右端の（L）は形状関数がLagrange族であることを示します
形状関数は当該節点の変位を1，その他の節点の変位を0とした場合の補間曲線を表します
実際の変位はこれらを自然座標から実座標へ写像（mapping）し係数倍したものの総和として与えます
- 作者: 久田俊明,野口裕久
- 出版社/メーカー: 丸善
- 発売日: 1996/01/01
- メディア: 単行本
- クリック: 3回
- この商品を含むブログを見る
