重み付き残差法 その5

前回に引き続き，今回は変分法 その2で扱った【カテナリー曲線】を，重み付き残差法を使って計算してみます
wrm3.wxm

y : 曲線
%o1にてパッケージ"mnewton"をロードします（画面出力は省略）
%o3にてyがxに依存することを宣言します（画面出力は省略）
a = 1とした場合の支配方程式を%o4式に示します（変分法 その2を参照ください）
被積分関数Fの定義を%o5式に示します

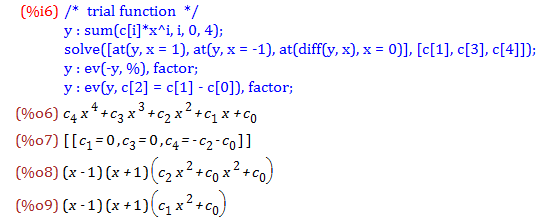
%o6式にて，試行関数yを任意の4次関数として与えます
2点[-1, 0]および[1, 0]を通り，x = 0における勾配を0とする境界条件より，%o7式を得ます
この結果で書き直したyを%o8式に示します（c[0], c[2]は未定係数）
ついでにc[0] + c[2] = c[1]として書き直します（%o9）

R : 残差
試行関数yを使って計算したFを残差Rとして%o10式に示します
重み関数に試行関数y自身を使います（ガラーキン法）
Rを未定係数c[0], c[1]で偏微分したものをそれぞれw[1], w[2]として%o11, %o12式に示します
区間[0〜1]で積分した重み付き残差の停留条件を%o13, %o14式に示します
上2式を非線形連立方程式としてc[0], c[1]について解いた数値解を%o15式に示します
上の結果よりyは%o16式となります

実際にグラフに描いて確認してみましょう（'A`)
ガラーキン法で求めた数値解を青線で，変分法による解を赤線で%t17にプロットします